Fracture mechanics analysis of topology-optimized parts
Written by Mark Oliver
Published on March 15, 2021
This article shares an example of using nTop to optimize a part and export it as a CAD body, then using Abaqus to calculate the stress intensity factor of cracks that develop perpendicular to the highest tensile principal stress.
The application of fracture mechanics to topology optimized parts is becoming increasingly important as topology optimization gains wider industrial adoption and is used in the design of more structurally critical components. One of the practical challenges of using fracture mechanics to analyze cracks in parts generated using topology optimization has been that the resulting geometry is typically in the form of a tetrahedral mesh rather than a CAD body. This prohibits the partitioning and swept meshing required to make fracture mechanics calculations using the finite element method. nTop addresses this challenge by enabling the conversion of topology optimization results into CAD bodies that can be readily partitioned and meshed as needed.
Part optimization and CAD body generation using nTop
Consider the design of a lever with nTop as shown in Figure 1. First, a linear finite element analysis of the initial part is built and solved. Figure 1a shows the von Mises stress in the lever under the prescribed loading. Second, topology optimization is used to cut the volume of the optimization domain by 50% while minimizing structural compliance. The topology optimization solution is shown in Figure 1b. Note that the volume around the three loading pins of the lever was excluded from the optimization domain. Next, the topology optimization solution is converted into an implicit body and smoothened to generate the part shown in Figure 1c. Finally, this smooth body is meshed (Figure 1d) and converted into a CAD body (Figure 1e).
nTop can export the CAD body shown in Figure 1e as a .step or .x_t file. The next section will show how the ability to export a CAD file enables the partitioning and structured meshing required to analyze cracks using the finite element method.

Figure 1. Generating an optimized lever CAD body in nTop.
Fracture mechanics analysis in abaqus
The CAD body created in nTop was imported into Abaqus and virtual topology was used to combine CAD faces so that the part could be partitioned and meshed as needed. The next step in this analysis was to calculate the stresses in the uncracked part to determine the location and orientation of likely cracks. Cracks tend to form on the surface of a part at the location of the highest tensile principal stress and then propagate perpendicular to that principal stress direction. Figure 2 shows the maximum principal stress contour in the lever. The most likely crack initiation site is indicated by the black arrow. The cross-section in Figure 2 shows the direction of maximum principal stress and the dashed black line marks the anticipated crack growth plane.
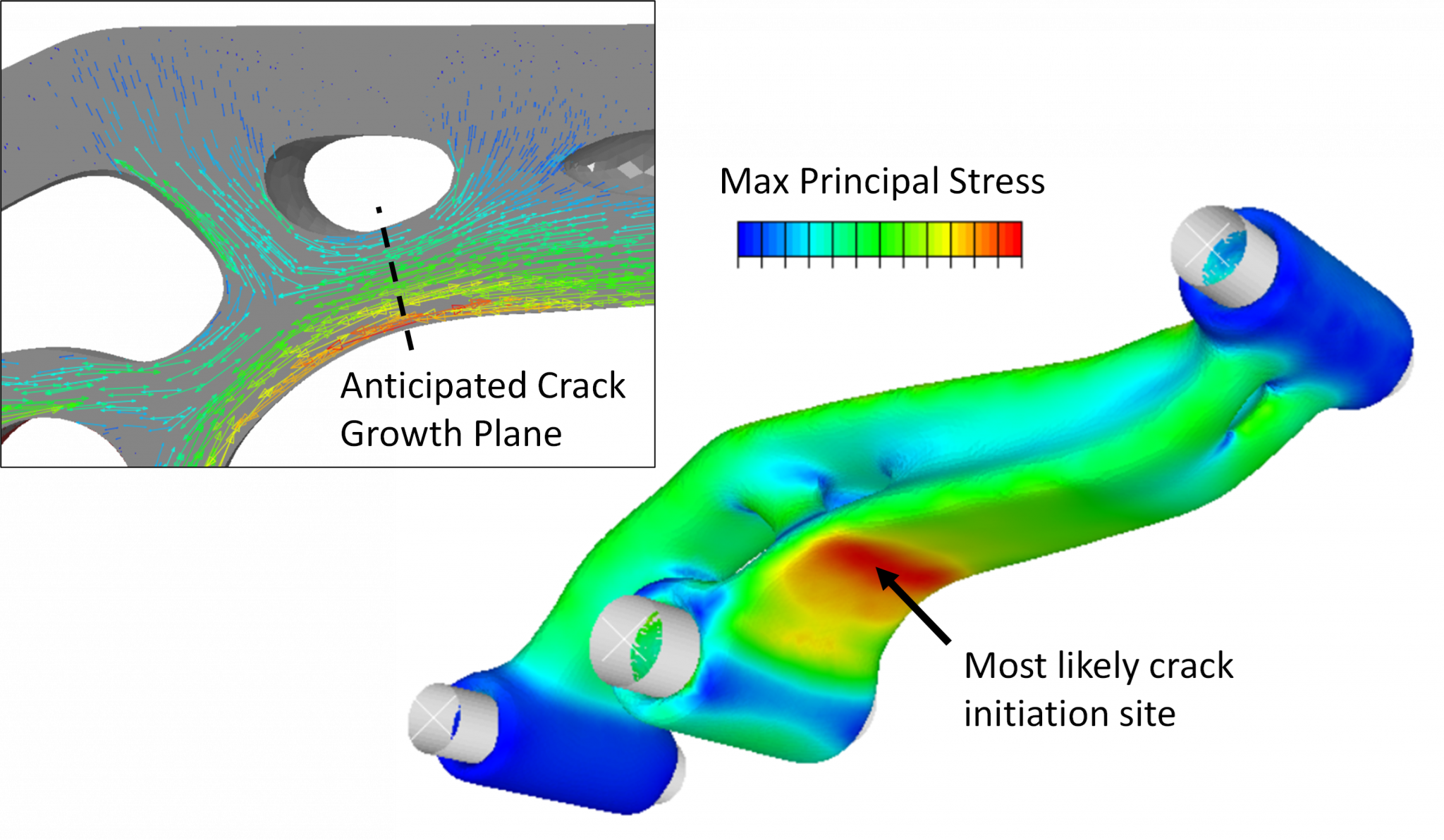
Figure 2. Max principal stress in lever showing the most likely location of crack initiation and plane of crack growth.
The part was then portioned along the anticipated fracture plane and a crack was added to the model. Calculation of stress intensity factors using the finite element model requires a swept mesh around the crack tip. The portion of the part around the fracture plane was therefore further partitioned so that an appropriate mesh could be generated. The ability to efficiently add a crack to the model and build the required mesh is enabled by having the topology optimized parts as a CAD body. The mesh around the crack tip is shown in Figure 3 with the crack front highlighted by the yellow line.
The von Mises contour of the cracked part is shown in Figure 3 along with a cross-section of the loaded crack. The stress intensity factor was calculated to be 51.7 MPa√m at the surface and 30.1 MPa√m at the deepest point of the crack. If the fracture toughness of the material is greater than 51.7 MPa√m, the modeled semicircular crack will be stable under the prescribed loading. Otherwise, the crack would cause the part to fail.
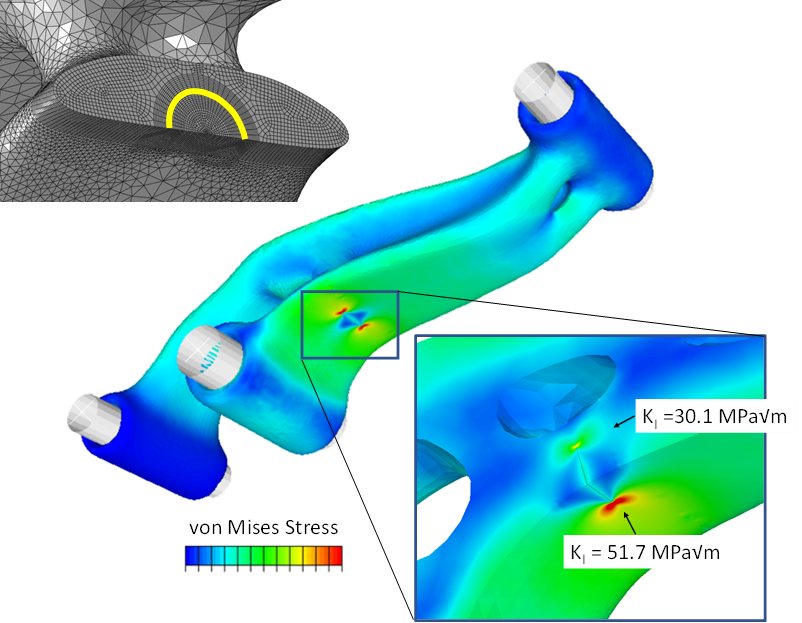
Figure 3. Analysis of a crack in the topology optimized lever.
Conclusion
Accurate analysis of cracks in topology optimized parts is becoming increasingly important as topology optimization gains wider industrial adoption and is used in the design of more structurally critical components. This requires using design software capable of creating manufacturable geometries and converting optimization results into CAD bodies. This article demonstrates how this workflow can be readily accomplished by coupling the capabilities of nTop with Abaqus.

Mark Oliver
Dr. Mark Oliver is a Managing Engineer at Veryst Engineering. Dr. Oliver has expertise in the materials science, solid mechanics, and failure analysis of metals, polymers, fiber-reinforced composites, adhesives, and additively manufactured materials. He is experienced in chemical and microstructural characterization, mechanical testing, and finite element analysis, applying his knowledge to issues of materials selection, mechanical design, and root cause determination of material failures. He holds a Ph.D. in Materials Science and Engineering from Stanford University.




