B-rep vs. implicit modeling: Understanding the basics
Written by Blake Courter | nTop
Published on March 12, 2019
Recently we introduced the concept of geometric modeling using an implicit representation, which permits robust operations and the ability to work with many sources of input data. Our flagship product, nTop, uses implicit modeling to generate functional designs from CAD geometry, simulation output, and topology optimization results, generating precise geometry and toolpath data for additive manufacturing and CAM.
Today’s B-rep and mesh-based modeling technology has enabled decades of innovation but has resisted automation and failed to address the complexity of advanced manufacturing. Common modeling operations such as rounds, offsets, and even booleans often fail, requiring special handling by skilled CAD users. Implicit 3D models are based on a different type of math that never fails, enabling the complete automation of advanced parts. In addition, implicit models can be directly coupled to less tangible input data such as simulation results and environmental measurements, producing variable thicknesses and nuanced geometry that’s almost impossible to achieve in traditional tools.
To understand how such benefits are possible, let’s compare the math behind B-rep and implicit modeling and examine why implicits can be reliable where B-reps and meshes fail.
Precise B-reps
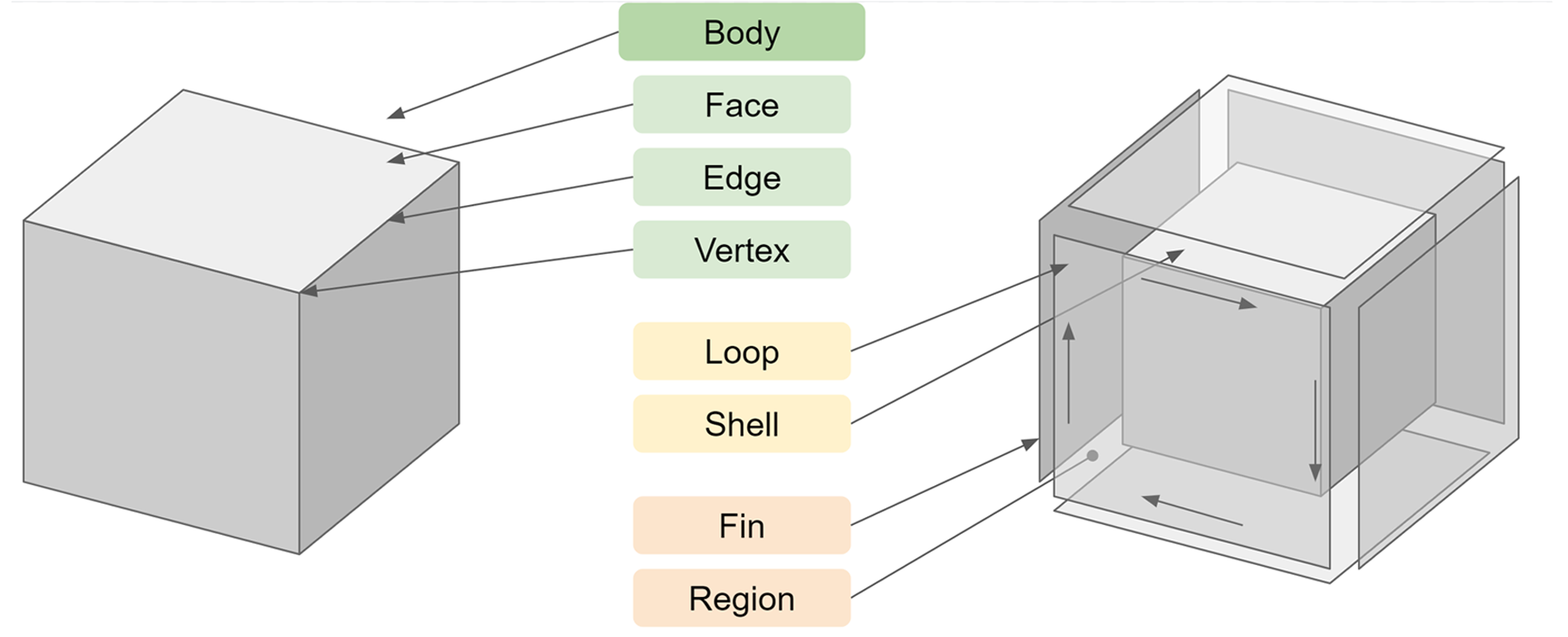
Precise boundary-representation (B-rep) solid models power most popular mechanical design tools, as they were the first technology to represent nominal geometry to within micron accuracy. They represent solids as a patchwork of faces joined together by edges that separate a homogeneous inside from the outside. Each face can be made of geometry appropriate for its contribution to the boundary of the part, such as a plane, cylinder, or spline surface.
The faces, edges, and other “topology” of B-reps are the main objects with which most CAD users interact. The paradigm works well for CAD models of low-to-medium complexity. Manufacturing features such as rounds, thin walls, and draft angles can be challenging to model, producing models whose complexity overwhelms the performance and usability of the paradigm. Although B-reps work well for common machined, formed, and molded parts, highly detailed designs, organic shapes, scan data, lattice and porous structures, spatially varying materials, and additively manufactured parts are not well represented by B-reps.

B-rep models consist of topological objects (informally, “topology”), which are backed by an underlying shape or geometry, in this case all planes for faces and lines for edges, etc. The objects in green at the top of the list are commonly exposed in the user interface of CAD systems. Lower level concepts, listed towards the bottom, are typically only exposed in CAD APIs.
B-reps are commonly exchanged via neutral formats such as STEP or native formats from component modeling engines such as Parasolid or ACIS. B-reps become impractical to work on when they have thousands of faces and impossible to work on when they have tens of thousands.
Meshes
Mesh models are simplified B-reps where all faces (typically called “facets”) are triangles. The more curved a region of the model is, the finer the triangles must be to represent it. The data structures tend to be simpler, in part because each facet’s planar geometry and boundary is described by the triangle. They also tend to lack the concept of regions or even separate shells, relying on the loop direction of the triangle to specify face orientation.

A precise B-rep model (left) and a low resolution mesh created from it (right).
Common mesh formats include STL, OBJ, and VRML. For manufacturing, meshes tend to become impractical when they have face counts in the tens of millions. Converting a B-rep to a mesh is typically straightforward, but due to lower resolution of mesh data, converting a mesh to B-rep is rarely more viable than remodeling.
For the rest of this post and blog series, we’ll use the term “B-rep” to refer to both the precise and mesh variants unless otherwise clarified.
Distance fields
How else might one model a solid shape other than by representing its boundary, piece-wise? The job, as stated above, is to simply know the difference between the inside and the outside of the model.
What if we had a kind of space where we could simply turn on or off bits of space, each its own cell or “voxel”, to denote what part of space is our part and what is not? That would work, but it would take a lot of voxels to achieve smooth surfaces. The orientation of the coordinate system also has an effect on surface finish, creating aliasing, which means that rotations would degrade the model.
A distance field takes that idea one step further. Instead of setting an on or off value, let’s store the distance to the boundary of the part we are trying to represent. Our model is then defined by a scalar field instead of a boolean field. We’ll use a sign convention that if we’re inside the part, the value will be negative, which makes the distance value continuous and differentiable at the zero-crossings that define the boundary of our shape. This representation, known as a signed distance field (“SDF”), packs a lot of power into a very simple concept.
Visualizing distance fields
Although both voxels and distance fields represent a shape using information distributed throughout space, they work and behave differently. The idea of a solid makes sense in any number of dimensions, so let's get a feel for distance fields using a 2D example of relatively simple shape, a capital R with serifs.
The B-rep version of the R is very similar to a 2D profile one would draw in a sketch or with curves in CAD, represented as segments of curves. We can then take that shape and convert it to pixels or a richer distance field representation:

2D pixel bitmap of a Times New Roman capital R glyph, and the same glyph converted to a 2D distance field and color-mapped to show constant distance.
Notice the white lines indicate constant distance in the distance field look just like offset contours of the shape. Indeed, a distance field encodes all of the information needed to instantly offset an object.
Another way to visualize the distance field is by using an extra dimension to hold the field value. Think of the distance field lines in the image above as a topographical map, which we can metaphorically reconstruct into an R-shaped island in a flat sea, where sea level represents our shape:

A 2.5 dimensional representation of a 2D distance field, where the plane shows the zero values (right), and offsetting the shape outward by lowering the plane.
Offsetting happens by raising or lowering the sea level. If the tide rises, our R becomes offset inward, and if the sea lowers, it becomes offset outward.
Distance fields of 3D solids work exactly the same way, and can be informally thought of as 3.5 dimensional entities. Notice, for example, that the R above has equally sloped or drafted sides. True distance fields always have that constant slope property.
Implicits versus distance fields
If you’re familiar with fields, you might be wondering, does the field need to be based on distance? In general, no, and we’ll use the term “implicit” to refer to any scalar field that defines a shape by the non-positive values of a field. For example, the two major kinds of topology optimization, based on either level sets or SIMP, uses distance fields or arbitrary scalar fields, respectively.
For the rest of this post, we’ll focus on the subset of those shapes where the slopes are constant and therefore represent a true distance field. In nTop, implicits such as top opt and simulation results can be converted to the more convenient distance field representation.
We mentioned that B-reps fail to scale as their amount of topology increases. How do implicits and distance fields scale? It turns out that there are many ways to represent implicits, using functions, voxel-like structures, finite element structures, and other techniques. nTop’s new approach to implicit modeling lets you generate output for CAD, CAE, and CAM at the required high tolerances for each.
A simple example
What do these different representations actually look like under the hood? Let’s take a very simple example, a circle in 2D, centered at the origin.
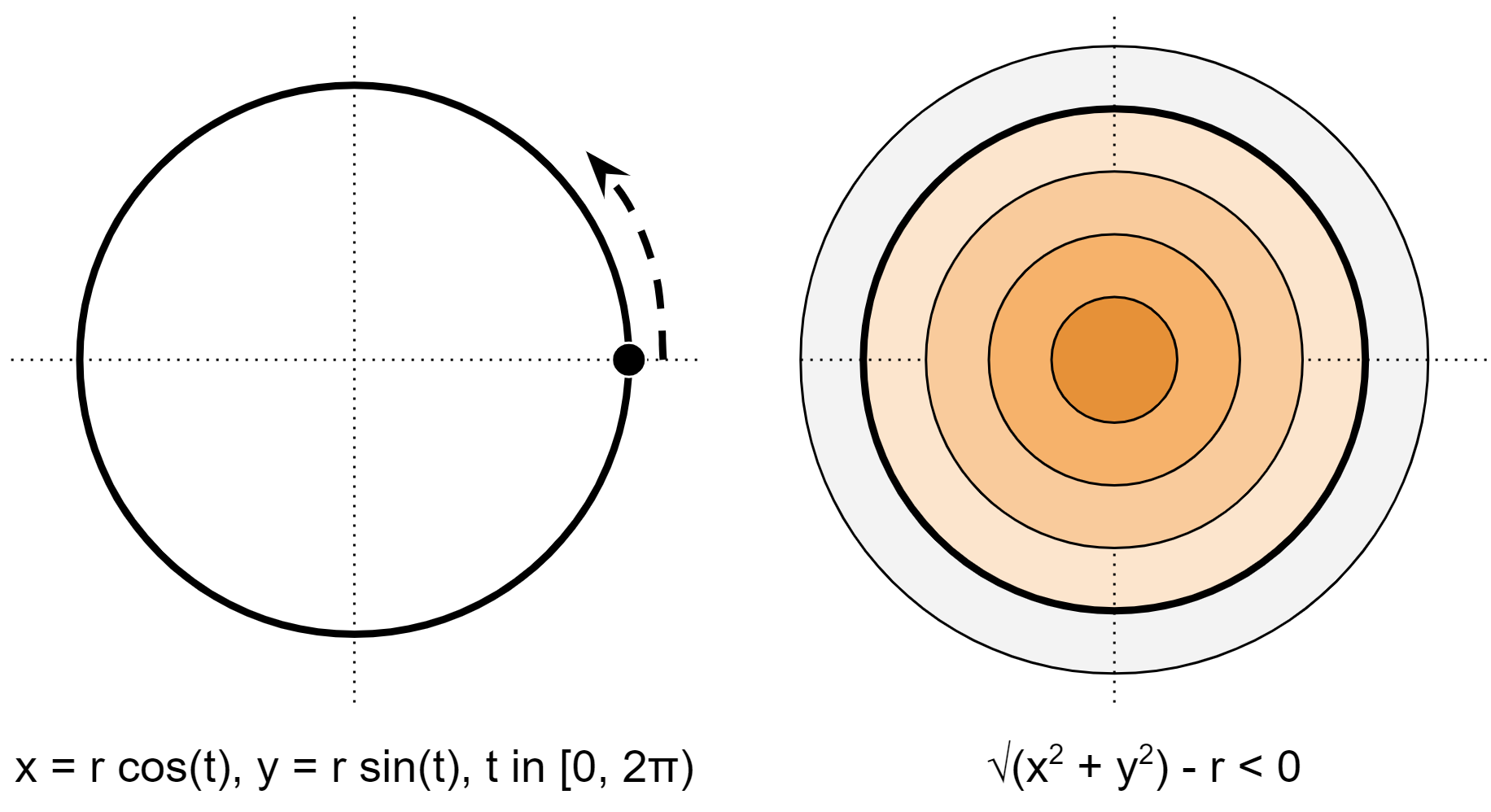
A circle represented in a B-rep (left) and a distance field (right).
To represent a circle as a boundary, we need to describe that boundary as a parametric curve, meaning that a single parameter traces out the boundary of the circle over this range with matching start and end points. In this example, there’s only one point to keep track of, so it’s straightforward. For more complex 2D shapes, every start point of one curve must match the end point of the next.
For the implicit circle, one must calculate the distance to the circle, which is the distance to the center minus the radius. Notice that this function is properly signed and is in fact a distance field.
The main practical difference between these functions is that the boundary version only defines information on the circle itself. Information about every other point in space is an extra calculation. In the implicit case, every point in space knows exactly how far it is from the nominal surface, providing a more complete view of the shape.
Summary
Distance fields encode extra information that radiates through space about where every point is in relation to that shape. That information turns out to make modeling operations more robust, which is the topic of our next blog post in this series on implicit modeling. In the meantime, if you want a more technical treatment of the math and theory behind these reps, I suggest this post from 0FPS.

Blake Courter
at nTop
Blake Courter is currently a Fellow at nTop and previously served as the company’s Chief Technology Officer, where he helped shape the core platform and technical vision. He brings deep expertise in geometric modeling, infrastructure, and advanced engineering software, and holds a BSE in Mechanical Engineering from Princeton University.




