Yamaha pairs topology optimization with graded lattices

Topology optimization and lattice structures can be combined to design parts with even higher added value. In this article, Hiroyuki Nagamoto, R&D Engineer at Yamaha Motor, explains how to use these two advanced engineering design techniques effectively. He walks us through a simple example and some practical design and manufacturing considerations.

Introduction

In advanced engineering design, topology optimization and lattice structures are often talked about in pairs. In recent years, tools like nTop and the concepts of Field-Driven Design have allowed engineers to realize designs with a higher degree of freedom. However, discussions have begun on how to use each approach properly.

Surface-based lattices (like gyroids and other TPMS structures) have high specific stiffness and are relatively easy to produce with additive manufacturing. Furthermore, lattice structures have many additional functional benefits, such as excellent heat exchange coefficient, high shock absorption, and excellent stiffness control. 

Using the added benefits of lattices, we can design parts with even higher added value than the shape obtained by pure density-based topology optimization.

- Hiroyuki Nagamoto, R&D Engineer at Yamaha Motor Co.

There are not many documents that quantitatively and clearly describe the functional superiority of the lattice structure yet. In this article, I would like to introduce a methodology to optimize a lattice structure for stiffness.

Example: Optimization of a beam

To start things simply, let us assume the problem where we apply evenly distributed loads to a double-sided iron beam. This single physics example showcases the functional superiority of the above design tools in a concrete way.

Topology optimization of double-sided beam

First, the topology is optimized based on the density method. The shape is output with the relative density threshold set to ρ = 0.5 and then smoothed using the Smooth Body block in nTop. The resulting volume of the part is 3990 mm3.

Zoom image

Next, we confirm the stiffness performance of the topology optimized shape using static analysis. We set up the simulation using the same loading and boundary conditions as in the topology optimization step. The maximum displacement in the loading direction is 2.152e-2 mm.

Zoom image

Functionally-graded lattice structure based on topology optimization

Let us now compare these results to the stiffness performance of a functionally graded lattice structure.

In examining the lattice structure, we adopted a “shell and infill” approach. The structure consists of an outer shell and an inner lattice structure. This configuration is bio-inspired and resembles the bone structure to improve the stiffness.

An example structure is shown in the figure below. Here, the topology optimization threshold was set to 0.4, and the outer shell thickness to t = 0.6 mm. We used a gyroid lattice with a cell size equal to 3 mm for the internal lattice structure.

Zoom image

The intermediate density distribution of the topology optimization controls the thickness of the gyroids (using the Ramp block in nTop) and is set to gradually change from 0.25 to 1.57 mm — thicker at sections with higher loading. The final volume was almost identical to the volume of the shape obtained from pure topology optimization.

Then we perform an analysis to confirm the part’s stiffness performance. The maximum displacement in the load direction was 2.008e-2mm.

Zoom image

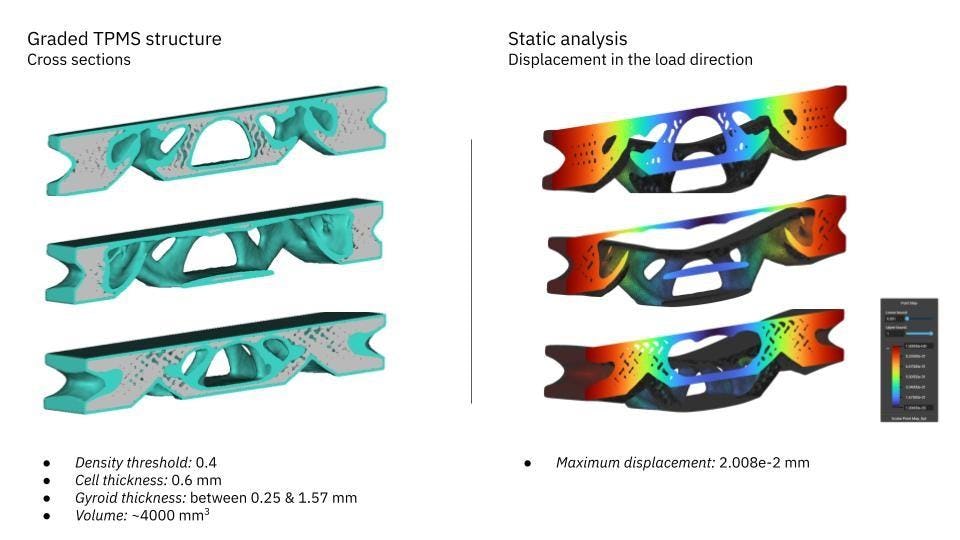
If we compare the displacement of the functionally graded lattice structure with the shape obtained by the pure topology optimization example of the previous section, we see that the stiffness is improved by about 7%.

Practical design considerations

Here are some practical design and manufacturing considerations that could help us expand this simple structural model and use it in real-world applications.

Automating design of experiments

As you can easily imagine, the stiffness performance of the lattice structure depends on many design parameters: the topology optimization density threshold, the selected lattice unit cell, the cell size, the beam diameter, the shell thickness, or the gradual change range of the plate thickness. 

Parameter optimization is required to find the optimum combination of them. Fortunately, since the command-line interface (nTop Automate) is implemented in nTop, optimization calculations can be executed by linking with tools such as modeFrontier.

Simulated vs. manufactured properties

The simulation showed that the lattice structure has superior specific stiffness. Still, in reality, some issues may arise that may cause the stiffness of the manufactured part to be different from that calculated in the analysis. This discrepancy is mainly caused by internal defects during Additive Manufacturing. 

This tendency is particularly noticeable in surface-based lattices (like gyroids and TPMS lattices). Research has shown that the actual stiffness of test pieces manufactured by the SLM method is about 30% to 56% of the analysis.

Therefore, it is necessary to modify the design to deal with manufacturing issues to ensure the stiffness of the actual product. We can achieve this by increasing the selected relative density, reducing defects during manufacturing with closer quality control, and so on.

Is topology optimization the right tool?

Regarding the calculation method, some researchers have pointed out that although topology optimization based on the density method provides a shape that is easy to interpret in engineering, it is not strictly mathematically legitimate. With the development of advanced engineering design tools and AM technologies, it is now possible to model and manufacture shapes that include the density of gray zones between 0 and 1. Therefore, it may be necessary to implement a topology optimization based on the homogenization method that can obtain a truly optimum solution.

Key takeaways

This article shows that we can combine topology optimization and lattice structures to create a structural model with superior stiffness performance through a simple example. 

We can create a structure with better specific stiffness than the shape obtained by the density-based topology optimization method because surface-based lattices have high specific stiffness and reproducibility of intermediate density. In the future, we can expect that the above DfAM technology will be used to create many innovative products and designs in various industries.

It is primarily due to the development of advanced design tools that engineers can quickly study such complex lattice structures. We are grateful to nTop, which is speedily developing the functions of such tools.

- Hiroyuki Nagamoto, R&D Engineer at Yamaha Motor Co.